Understanding Octaves
In many audio reviews, particularly those that
evaluate loudspeakers, reviewers frequently refer to octaves; e.g.,
"this speaker does not quite reach down into the bottom octave." But what is an
octave, really, and how does it relate to frequency response?
In music theory, an octave is the interval between two
notes that sound very much alike, though one is higher in pitch than the other. Two notes
an octave apart are given the same note name -- A, B, C, etc. -- and are considered to be
in unison. But octaves do not exist only in music theory. There is a physical basis
for why these notes sound similar. There are, basically, two ways of obtaining this higher
pitch from a vibrating object. The first way is to cut the size of the object (e.g.,
a string or organ pipe) exactly in half. The second way is to cause the object to vibrate
exactly twice as fast, which creates a node halfway along the vibrational axis, much as if
there were now two half-size objects vibrating.
We can do a little experiment. For this exercise,
we’ll need an empty beer bottle. (To ensure the integrity of the bottle, it might be
wise to start with a full one and drain it according to proper procedures -- cheers!)
Everyone knows that blowing across the mouth of a bottle produces a pitch that is
determined by the volume of the bottle. (Helmholtz’s equation lets us calculate the
frequency of that pitch.) But did you know that you can produce the pitch one octave
higher than that fundamental frequency without changing the bottle’s volume?
Take a deep breath, then blow air twice as fast across the mouth of the bottle. If you do
it properly, you’ll be rewarded with a loud, shrill sound that’s likely to get
you thrown out of the bar. Don’t say I didn’t warn you.
Why do two notes an octave apart sound similar? We can make
a graph to represent the two soundwaves, with time along the X axis and amplitude on the Y
axis. The lower pitch (100Hz) is shown in blue, and the pitch one octave higher (200Hz) in
red.
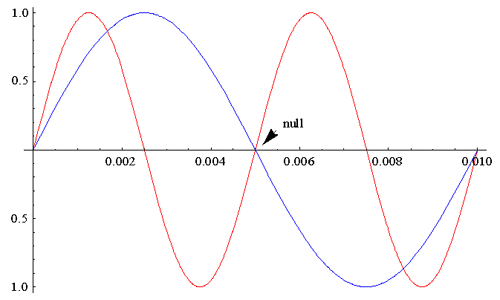
Note that the faster frequency intersects the slower at
every one of its null points. It is this consonance that causes the ear-brain
apparatus to interpret the two sounds in the same manner. To hear the addition of octaves,
here is a WAV file that begins with
a pure 220Hz tone, and adds one octave each second.
In physics, the definition of an octave is the
doubling in frequency of a vibration. As mentioned above, notes that are an octave apart
are given the same name -- A, B, C, etc. (or Do, Re, Mi, etc.). In the absence of harmony,
the octave of each note is irrelevant. If two singers -- a soprano and a tenor, for
instance -- sing the same melodic line an octave apart, it sounds almost as if they are
singing exactly the same thing -- and, from a music-theory point of view, they are.
Harmony is the addition of notes separated from the melodic line by any interval other
than an octave. When harmony is added to a composition, the respective octaves of each
note become more important. A C accompanied by the G above it sounds
different from that same C accompanied by the G below it.
There are, primarily, two conventions used to distinguish
between named notes in different octaves. First, let us orient ourselves to the so-called
"middle C." While this note lies roughly in the middle of a piano keyboard,
it’s called middle C because it lies in the middle of the grand staff in musical
notation, exactly between the treble and bass clefs. The frequency of middle C is
approximately 262Hz.
Helmholtz notation refers to middle c as c’,
the note one octave below it as c, the note an octave below that as C, and
the lowest c on the piano as CC. Ascending from middle c, we have c’, c’’,
c’’’, and c’’’’. The note one semitone
below middle c is b, and the note one octave above b is b’. The
precise way in which these notes are written can vary, such as using ci
instead of c’, and Ci instead of CC.
The other method, called Scientific Pitch Notation, gives
the note name followed by the octave number. In this system, middle c is called C4.
The note one octave below middle c is C3, and the note one octave above middle c is
C5. The lowest c on the piano is called C1, and the two notes below it are B0
and A0. In this notation, the note one semitone below middle c is called B3,
and the note one octave above is B4.
The complex harmonies of an orchestral composition, or even
one for solo piano, cover not just two or three, but many octaves. In order for all of
those sounds to be reproduced in the manner intended by the composer and performers, a
loudspeaker must be able to produce the same range of frequencies as the orchestra, piano,
rock band, synthesizer, etc.
It is commonly accepted that the lowest note the human ear
can hear has a frequency of 20Hz. Convention may vary from reviewer to reviewer, but in
most cases, when a reviewer writes about the lowest octave, he is referring to the
frequencies from 20Hz to 40Hz. Doing some quick calculations, we find that 20Hz lies
between D#0 and E0, and 40Hz lies between D#1 and E1. The
lowest note on the manuals (the keys played with the hands) of an organ is CC, or C1,
at 32.7Hz. This note is also the lowest c on the piano keyboard. Although most
floorstanding loudspeakers can reproduce C1, the output levels of many smallish
towers may be quite reduced at this frequency. The lowest note on a standard piano is A0,
or 27.5Hz. (Some Bösendorfer pianos have an extended keyboard of 97 keys that reaches all
the way down to C0.) On an organ, the notes below C1 are played with foot
pedals, and consequently are often referred to as pedal notes. A typical organ can
play, by means of the pedals, down to C0 (16Hz), and many can play a full octave or
more below that, although at this point the notes are infrasonic -- that is, they
are more felt than heard. Only very large, well-designed loudspeakers are capable of
reproducing even the higher pedal notes.
Not every audiophile is an organ fan, so let us briefly
examine the lower-pitched instruments of a symphony orchestra to see where they fall in
the frequency range. A string bass, sometimes called a double bass, can play down to G1
(49Hz); with an extension, it can reach C1 (32.7Hz). The bass tuba and
contrabassoon also play in the C1 octave. Some percussion instruments, such as the
timpani, can be tuned to these pitches, and a very large bass drum can play quite a bit
lower.
Hopefully, the information above will give you some
guidelines in choosing which speaker can reproduce the notes that are important in the
type of music to which you like to listen. It’s important to remember that the +/-3dB
specifications don’t tell the entire story of frequency response. If a speaker rolls
off gradually, you may find that a lower specification of 40Hz does, in fact, let you hear
C1, though with a little less power than the higher pitches. The SoundStage!
Network publishes speaker measurements to help you get a better feeling for what lies
behind those single numbers.
To explore the high end of a speaker’s response, we
must delve into the fascinating topic of harmonics, which is the subject of a future
article.
...S. Andrea Sundaram
|